Boyer-Moore majority vote algorithm

Problem

Given a sequence of elements, the task is to find the majority (elements that appear more than half of the total) of the sequence.

Algorithm

The algorithm keeps track of two variables: count and candidate.

• count: Initially set to zero. Indicates how many times candidate has left until being replaced.
• candidate: Possible majority element.

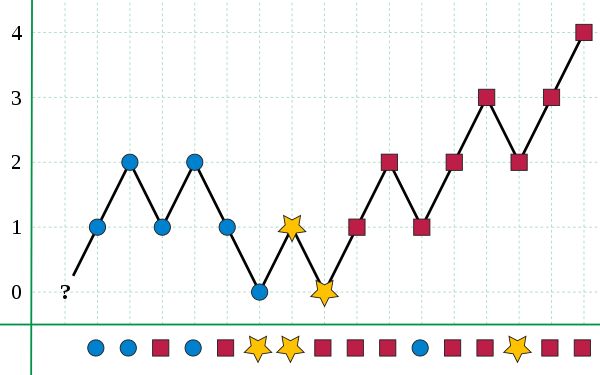
Below is the python code of the Boyer-Moore majority vote algorithm.

def boyer_moore_majority_vote(arr: List[int]) -> int:
    count, candidate = 0, 0
 
    for elem in arr:
        if count == 0:
            candidate = elem
        if candidate == elem:
            count += 1
        else:
            count -= 1
 
    return candidate

Its time complexity is $\mathcal{O}(n)$, where $n$ is the number of elements. Its space complexity is $\mathcal{O}(1)$, as it only needs the space for two local variables.

The algorithm will, however, return one of the elements even when the input sequence has no majority. Thus, one must perform a second pass to verify whether or not the returned element is actually a majority.

References

• Wikimedia Foundation. (2024, January 1). Boyer–Moore majority vote algorithm. Wikipedia. Retrieved January 13, 2024, from https://en.wikipedia.org/wiki/Boyer%E2%80%93Moore_majority_vote_algorithm